K Nearest Neighborinoes

One of the most fundamental problems in machine learning is the problem of classifying data. In the set up of this problem we are given n pairs (\(X_1,Y_1\)), ..., (\(X_n,Y_n\)) where each \(X_i\) is an element of \(\mathbb{R}^{d_1}\) and each \(Y_i\) is an element of \(\mathbb{R}^{d_2}\). Here \(X\) is the data and \(Y\) is it's class. As an example one popular dataset that is used is the MNIST dataset where the data is the pixel values of the \(28\times28\) image of a hand drawn digit and the class is the digit of the image (for example if the digit that is drawn is four it will have a \(Y\) value of \(4\)).

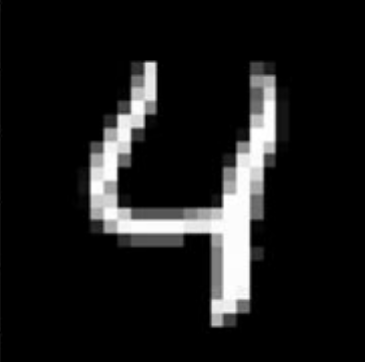
Now the problem is how can we predict what class new data should be placed in. A commonly used solution to this is the K nearest neighbors algorithm. There are four main steps in the algorithm:

1. Calculate the distances from the new data input to all the data that has already been classified

2. Order the distances from shortest to longest giving a list of distance values from the nearest neighbor to the farthest neighbor

3. Using a prespecified value of k we abridge our list to the k closest distances

4. The class that apears the most often in this list is the one we classify our new data as

One important thing to note in step 2 is that we do not necessarily need to use the standard Euclidean distance and can define other distance measures. A distance function \(d(x,y)\) must only satisfy a few properties:

1. \(d(x,y)=0\) if and only if x=y

2. \(d(x,y)=d(y,x)\)

3. The triangle inequality \(d(x,z)\leq d(x,y)+d(y,z)\)

The above properties can also be used to show that \(d(x,y)\geq0\). What is commonly used in place of the Euclidean distance is it's generalisation defined as:

\(d_{p}(\textbf{X}_1,\textbf{X}_2)=||\textbf{X}_1-\textbf{X}_2||_{p}\)\(=\left(\sum_{i=1}^{n}|X_{1i}-X_{2i}|^{p}\right)^{1/p}\)

The case of p=2 is the Euclidean distance, the case of p=1 is the Manhatten distance and in general is known as the Minkowski distance.

One important question that you may now have is how do we choose the best distance function and k value to use? For the k value small values of k are extremely sensitive to noise whereas large k values will eliminate the noise although there may be some difficulties introduced if there is significant overlap between two or more classes. Generally a k value of around 5 produces a good result however to find the best value the algorithm needs to be run within a range of mutiple different k values that is reasonable for the given dataset in order to find the best k value. The best distance function to use will depend on the data. For example the Hamming distance (p=0) is used when the data is categorical. Nonetheless the Euclidean distance will generally be the most appropriate as it deals with numerical data rather well. For more of an explanation you can view (1).

This algorithm has a few significant disadvantages. The first is that the computation time increases proportionally with the amount of data that is available. This may cause the calculation of all the distances in an extremely large data set to become infeasable. The other major disadvantage is that the best value of k always needs to be calculated meaning that the algorithm needs to be run through multiple times. The final major disadvantage is that if the units that the classes are measured in are on different scales (e.g. cm vs km) then the algorithm will have a poor performance.

Now using the MNIST dataset I will provide an example implementation of the KNN algorithm. First pytorch is imported and used to load the MNIST training and test set data. The data is also reshaped to put all the pixel values into a single vector. It is important to note that there are 60000 images in the training set and 10000 in the test set.

import torch
import numpy as np
from torchvision.datasets import MNIST
mnist_tr = MNIST('~/.torchvision', train=True, download=True)
x_train, y_train = mnist_tr.data.unsqueeze(1).type(torch.FloatTensor)/255, mnist_tr.targets
mnist_ts = MNIST('~/.torchvision', train=False, download=True)
x_test, y_test = mnist_ts.data.unsqueeze(1).type(torch.FloatTensor)/255, mnist_ts.targets

xt = x_train.reshape(60000,784)
xts = x_test.reshape(10000,784)

Sklearn is now imported so that the KNN algorithm can be used and its accuracy calculated.

import sklearn
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report

The model is defined as KNeighborsClassifier with the parameter n_neighbors being set to the current k. The model is then fit to the training data and then the testing data is run on the model. The score of this is then returned as value between 0 and 1 (multiplying by 100 gives the accuracy percentage). This is appended to the accuracies list and the loop repeats until all the k values 1 through 14 have been tested. The code below also returns the index of the most accurate k as the variable i.

kVals = range(1, 15)
accuracies = []

for k in range(1, 15):
    model = KNeighborsClassifier(n_neighbors=k)
    model.fit(xt, y_train)
    
    score = model.score(xts, y_test)
    print("k=%d, accuracy=%.2f%%" % (k, score * 100))
    accuracies.append(score)
    
i = int(np.argmax(accuracies))
print("k=%d achieved highest accuracy of %.2f%% on test data" % (kVals[i],
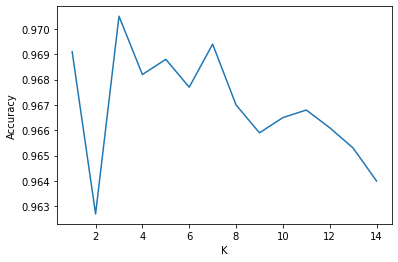
    accuracies[i] * 100))

Here matplotlib is imported and the accuracy is plotted against the k value.

import matplotlib.pyplot as plt

domain = np.linspace(1,14,num=14)

plt.xlabel("K")
plt.ylabel("Accuracy")
plt.plot(domain,accuracies)
plt.show

The noise that remains at k=1 and k=2 lowers the accuracy before reaching a peak around k=3 to k=7. Above k=7 the accuracy begins to decrease as there is likely overlap between the classes being introduced. Despite this the algorithm still has an extremely high accuracy.

The code can be downloaded here. Save it and run it in a Jupyter notebook.

Further Resources

(1) Victor Lavrenko, K-NN 4: which distance function?,2014

Home