Learning Logic

One of the most popular class of models in machine learning at the moment are neural networks which have their origins in the humble Perceptron. The Perceptron proposed by Frank Rosenblatt was intended to model a single neuron and is capable of binary classification by "firing" if the data is of one class and not "firing" if the data is of the other class.

We model this behaviour via taking the dot product of the input data with the weights, which we must learn. We then take the sign of this dot product (sign function returns 1 if the input is positive and -1 if the input is negative) giving 1 if it's in the first class and -1 if it's in the second. So the function we use for classification is \(f(x)=sgn(x^Tw)\), where x is the data and w is the weights. For d-dimensional data we append a one to the top of the vector in order to account for a bias term in our weights (a bias term allows the boundary line to have an intercept that isn't the origin).

We now have a model but we need an algorithm to learn the weights. For this problem we are given \((x_1,y_1),...,(x_n,y_n)\in\mathbb{R}^{d+1}\times\{-1,+1\}\), where \(x_i\) is the data and \(y_i\) is its class label. We can begin training by randomly or smartly intialising weights (in the code I provide I initialise all the weights to 0). Once this is done we plug each \(x_i\) into \(f(x)\) and if it missclassifies the data we update the weights via the following rule, \(w\leftarrow w+\eta y_ix_i\), where \(\eta\in(0,1]\) is the learning rate.

We use this update rule as we know that \(x_i\) gets correctly classified if \(y_ix_i^Tw>0\) (i.e. it is correctly classified if the sign of the output is the same as the sign of \(y_i\)). So plugging the update into \(y_ix_i^Tw\) we get \(y_ix_i^T(w+\eta y_ix_i)=y_ix_i^Tw+\eta\lVert x_i \rVert^2>y_ix_i^Tw\) (note that \(y_i\cdot y_i=1\) as \(y_i\) is 1 or -1). Hence we see the update rule moves \(y_ix_i^Tw\) towards positive values, i.e. towards a correct classification. Given linearly seperable data we can thus repeat this update procedure until no data is incorrectly classified.

def perceptron(w, x, y, lr, maxiter):
    j = 0
    while (j < maxiter):
        misscnt = 0
        output = np.sign(x @ w)
        for i in range(len(output)):
            if (output[i]!=y[i]):
                w  = w + lr * y[i] * x[i]
                misscnt += 1 
        if (misscnt == 0):
            break
        j += 1 
    return [w, j, misscnt]
	    

Now with the Perceptron implemented we can teach it some functions, specifically for this article we will teach it the logic functions.

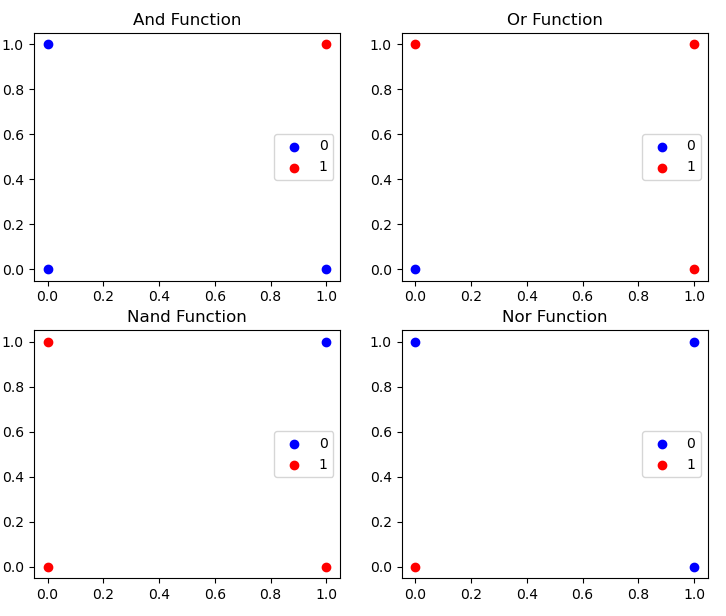
Each of these logic functions takes x and y as input (x and y are both either 0 or 1) and outputs 1 if the logic function returns true and 0 if it returns false (in the code for the Perceptron this will occur as a -1 so the sign function works with the class label). We see that each of these functions produces linearly seperable classes and hence the Perceptron can learn them. Running the algorithm on these functions yields the following output:

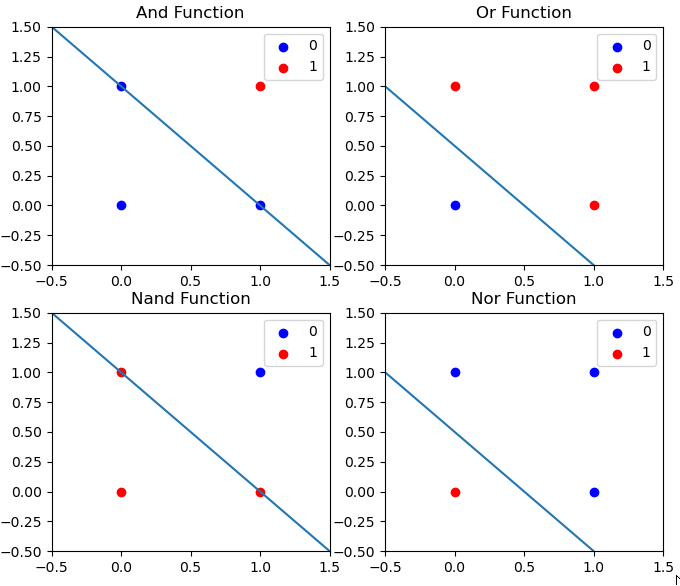
We get these boundaries from the learned weights vector \(w=(a,b,c)^T\) via the linear relationship \(0=a+bx+cy\iff y=-\frac{(a+bx)}{c}\). These aren't the only logic functions, we also have the exclusive or function.

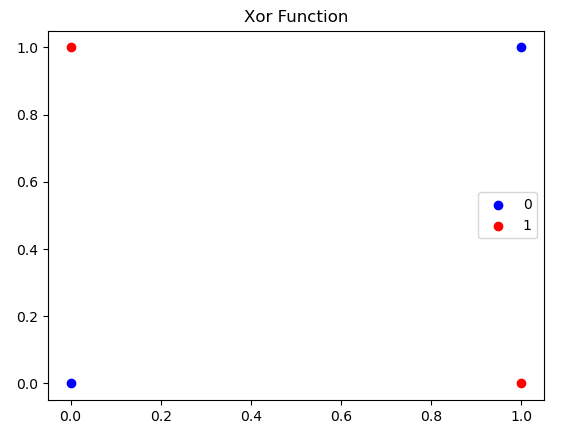
This now presents us an issue as the data can't be seperated via a line. We can work around this using the kernel trick. The kernel trick adds a dimension to the data by carefully constructing a function that will make the data linearly seperable in the increased dimension. In this case we will add a dimension to the data to make it linearly seperable via \(x_i=(1,a,b)^T\rightarrow x_i=(1,a,b,|a-b|)^T\). The function \(|a-b|\) is used as it returns 1 if a and b are different and 0 if they are the same. We can now learn a seperating plane for this appended data, giving:

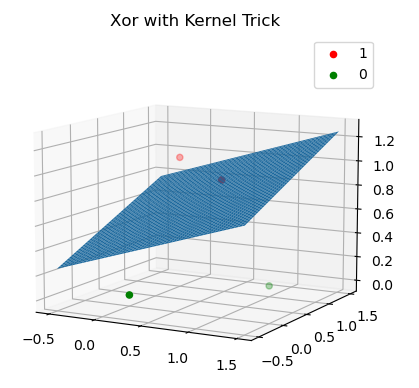We have now learned what a Perceptron is, implemented it in python and used it to learn logic functions. The source code for this article can be found here.

Home